
The presented techniques can be utilized to explore novel aspects of both classical and quantum dynamics in negatively curved spaces, and to realise the emerging models of topological hyperbolic matter. Our experiments showcase both a versatile platform to emulate hyperbolic lattices in tabletop experiments, and a set of methods to verify the effective hyperbolic metric in this and other platforms. We use a lattice regularization of hyperbolic space in an electric-circuit network to measure the eigenstates of a ‘hyperbolic drum’, and in a time-resolved experiment we verify signal propagation along the curved geodesics.
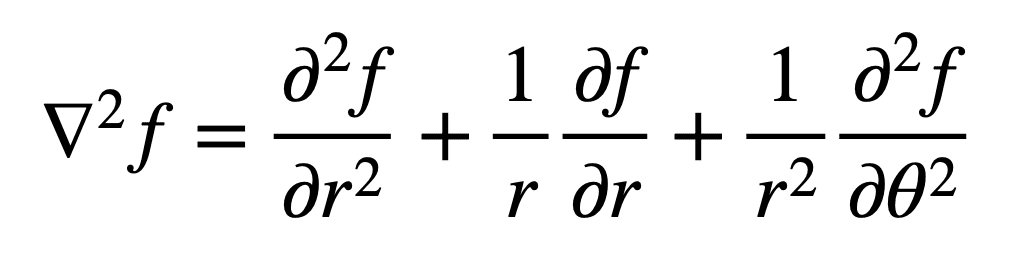
It is used widely in electrical engineering.

Here we discuss and experimentally demonstrate that the spectral ordering of Laplacian eigenstates for hyperbolic (negatively curved) and flat two-dimensional spaces has a universally different structure. The Laplace transformation involves integration, complex numbers, and exponential functions. According to Quantum Field Theory (QFT) in curved spacetime, the equation describing a behavior of particles around blackhole is Klein-Gordon Equation (K-G. Let us recall this particular definition.

A key input for the Laplace equation is the curvature of space. When it comes to Euclidean space, Laplacian is frequently defined as a second order differential operator acting on functions in a way that it assigns the sum of all unmixed second partial derivatives along coordinate axes in the Cartesian coordinates. In 5 we shall work on a general curved background and prove the following. The Laplace operator encodes the behavior of physical systems at vastly different scales, describing heat flow, fluids, as well as electric, gravitational, and quantum fields. We identify the symmetry algebra of the Laplacian on Euclidean space as.


 0 kommentar(er)
0 kommentar(er)
